Стереометрія – це розділ геометрії, який вивчає властивості геометричних фігур у просторі.

У стереометрії основними поняттями є точка, пряма і площина. Площину в геометрії вважають рівною та необмеженою. Вона не має межі та не має товщини. Площини позначаються грецькими буквами α, β, γ тощо. На малюнках нижче зображені тільки частини площин – у вигляді паралелограма та у вигляді довільної замкненої області:

Поняття про аксіоми і теореми (повторення)

Аксіома – це твердження, яке приймається на віру (без доведення). 

Наведемо кілька прикладів:

1) Яка б не була пряма, існують точки, які належать цій прямій, і точки, які не належать їй.

 

 

2) Через будь-які дві точки простору можна провести пряму, і тільки одну. (Аксіома проведення прямої в просторі)

 

 

 

3) Пряма розбиває площину на дві півплощини.

 

 

 

4) Із трьох точок прямої одна і тільки одна лежить між двома іншими.

 

 

5) Кожний відрізок має певну довжину, більшу за нуль.
6) Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його внутрішньою точкою.
7) Кожний кут має градусну міру, більшу за нуль. Розгорнутий кут дорівнює 180°.
8) Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами.
9) На площині через точку, що не лежить на даній прямій, можна провести лише одну пряму, паралельну даній.

Теоремою називають твердження про властивість фігури, істинність якого встановлюється в результаті міркувань. Ці міркування називають доведенням.

Наведемо приклад:

Теорема: Дві різні прямі можуть перетинатися тільки в одній точці.

Доведення

Якби дві різні прямі мали дві точки перетину, то через ці точки проходило б дві різні прямі. А це неможливо, оскільки через дві різні точки можна провести тільки одну пряму (за аксіомою 2). Отже, дві різні прямі не можуть мати дві різні точки перетину.

Поняття про обернену теорему

Будь-яка теорема складається із двох частин: перша частина – це умова (тобто те, що задано), друга частина – висновок (те, що треба довести).

Візьмемо такий приклад.

Якщо дві різні прямі перетинаються (умова), то вони мають лише одну спільну точку (висновок).

Якщо замінити місцями висновок і умову в теоремі, то одержимо теорему, обернену до даної. Дану теорему ще називають прямою.

Наприклад, теорема “Якщо дві різні прямі мають спільну точку (умова), то вони перетинаються (висновок)” є оберненою до теореми “Якщо дві різні прямі перетинаються (умова), то вони мають лише одну спільну точку (висновок)”.

Аксіоми стереометрії

Нагадаймо, що властивості основних геометричних фігур, які приймаються без доведення, називаються аксіомами.

Нижче мова буде йти про аксіоми, що виражають основні властивості прямих і площин у просторі. Так як поняття площина  потребує розширення систем аксіом, то це завдання реалізує нова група аксіом – група аксіом С .

Аксіома С I 

(Аксіома належності точок площини)

Аксіома С I. Яка б не була площина, існують точки, які їй належать, і які їй не належать. 

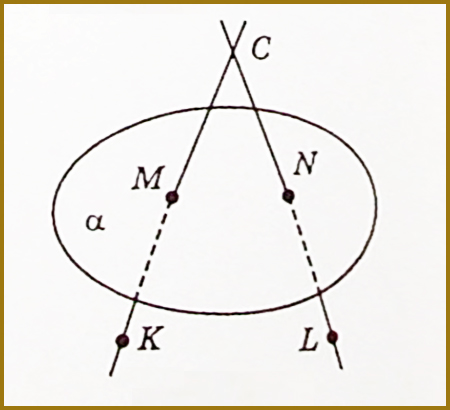
На малюнку  точки M і N належать площині α (площина α проходить через ці точки), а точки C, K і L не належать цій площині. Для запису цього використовують символи ∈ і ∉. Наприклад, M ∈ α, K ∉ α .

Аксіома С II

Аксіома належності прямої площині

Аксіома С II. Якщо дві точки прямої  лежать у площині, то всі точки прямої належать цій площині.

У цьому випадку кажуть, що пряма належить площині або площина проходить через пряму. Щоб записати це, використаємо символ підмножини: m ⊂ α.

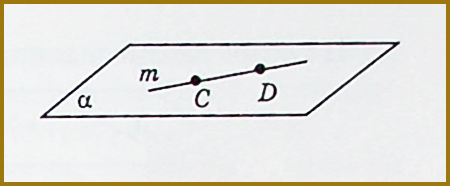
Роздивимося ще приклад з малюнком (мал. 2), який розкриває дану аксіому:

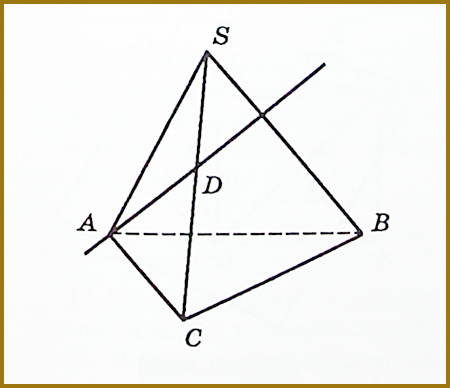
Так, пряма AD на малюнку 2 має дві спільні точки A і D з площиною грані SAC піраміди і тому лежить у цій площині.

Тепер роздивимося наступні малюнки:

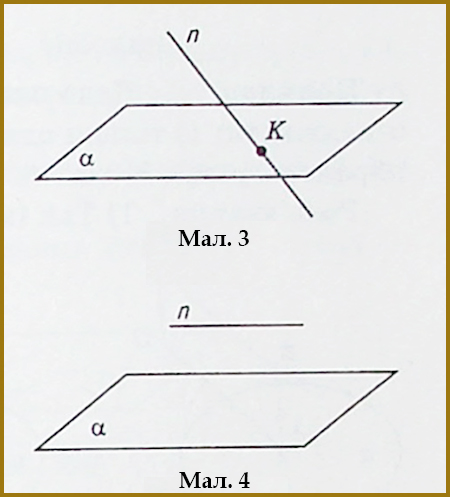
Запис n ⊄ α, означатиме, що пряма n не належить площині α (мал. 3 і 4), тобто існує така точка прямої n , яка не належить площині α . На малюнку 3 пряма n і площина α мають одну спільну точку K. У такому випадку кажуть, що пряма n і площина α перетинаються в точці K. Записують це так: n ∩ α = K .

Аксіома С III

Аксіома перетину площин

Аксіома С III. Якщо дві площини мають спільну точку, то вони перетинаються по прямій, яка проходить через цю точку.

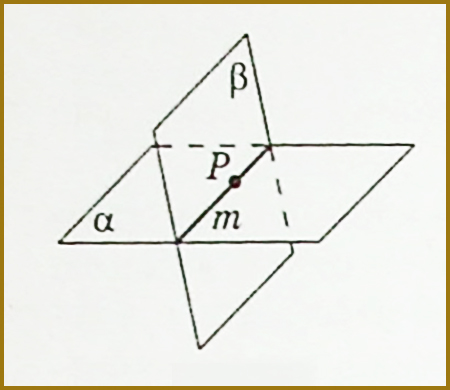
На цьому малюнку площини α і β мають спільну точку Р, тобто Р належить як площині α, так і площині β. Аксіома С IIIстверджує,  що площини α і β перетинаються по прямій m. Записують це так: α ∩ β = m . При чому точка Р належить прямій m через яку, в свою чергу, проходять дві різні площини α і β.

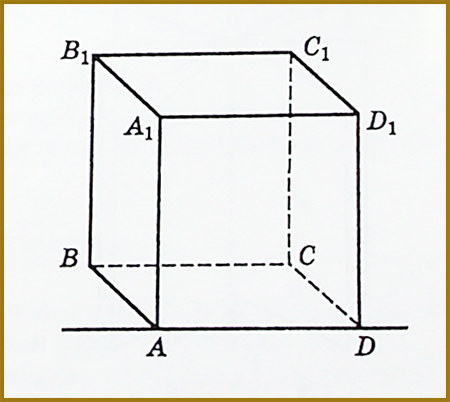
Площини граней 

\[ AA_{1}D_{1}D \]

 і ABCD куба (мал. 2) мають спільну точку А, тому вони перетинаються по прямій AD.

З аксіоми С III випливає, що через одну й ту саму пряму можна провести безліч площин. Давайте роздивимося наступний малюнок:

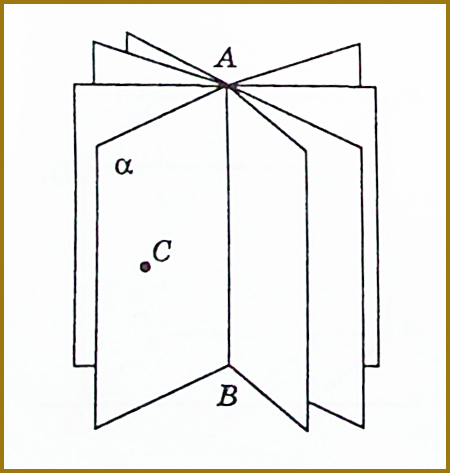
На цьому малюнку бачимо, що через пряму AB проходить чотири площини. Їх можна розглядати, як послідовне положення площини, яка обертається в просторі навколо прямої AB. Щоб виділити якусь із площин, наприклад площину α, треба зафіксувати точку С, яка не лежить на прямій AB.

Аксіома С IV

Аксіома проведення площини

Аксіома С IV. Через будь-які три точки, що не лежать на одній прямій, можна провести площину, і до того ж тільки одну. 

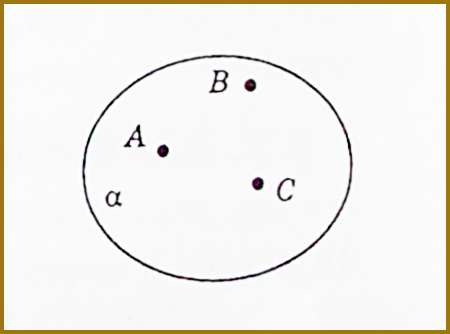
На цьому малюнку ми бачимо точки A, B і C, які не лежать на одній прямій. Площину, яка проходить через точки A, B і C (що не лежать на одній прямій), часто називають “площиною ABC”. Аксіома С IV стверджує, що існує одна площина α така, що A ∈ α, B ∈ α, C ∈ α .

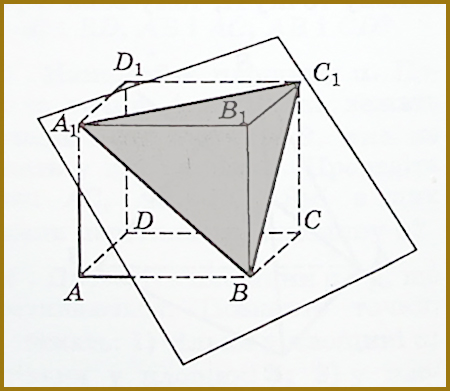
На цьому малюнку зображено переріз паралелепіпеда площиною

\[ A_{1}B C_{1} \]

Аксіоми стереометрії і наслідки з них

Наслідки з аксіом стереометрії формулюються у вигляді теорем.

Теорема 1

Теорема про проведення площини через пряму і точку

Теорема 1. Через пряму і точку, яка не лежить на ній, можна провести площину і до того ж тільки одну.

Доведення

Будь-які дві точки даної прямої разом разом з даною точкою утворюють три точки, що не лежать на одній прямій. Розглянемо пряму a і точку М таку, що М ∉ а. На прямій а позначимо довільні точки C і D. Оскільки C, D і М не лежать на одній прямій, то через них за аксіомою С IV , можна провести площину  α. Точки C і D лежать у площині α, а тому за аксіомою С II , пряма а належить площині α. Отже площина α проходить через пряму а і точку М.

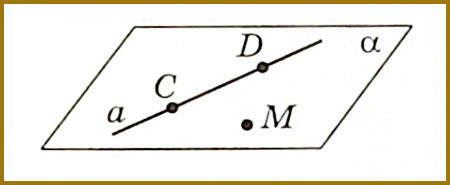
Тепер доведемо, що така площина єдина. Припустимо, що через пряму а і точку М проходить ще одна площина α1.  Але тоді ця площина має проходити і через точки C і D, що лежать на прямій а. Маємо, що через точки C, D і М, які не лежать на одній прямій, проходять дві різні площини α і α1, що суперечить аксіомі С IV . Отже таке припущення хибне, а тому через пряму а і точку М, що їй не належить, проходить єдина площина α.

Теорема 2

Теорема про проведення площини через дві прямі, що перетинаються

Теорема 2. Через дві прямі, що перетинаються, можна провести площину і до того ж тільки одну. 

Доведення

Розглянемо прямі a і b, причому a ∩ b =C.  Позначимо на прямій b точку М, а на прямій a – точку D, обидві відмінні від точки С. Маємо три точки М, С і D, які не лежать на одній прямій.

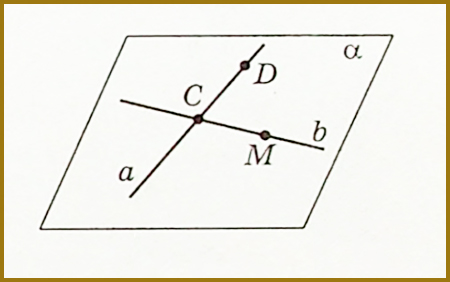
Тому далі доведення аналогічне до доведення попередньої теореми 1. Тому що точки і точка перетину цих прямих не лежать на одній прямій. Отож, через них проходить єдина площина (аксіома С IV), на якій лежать обидві прямі (аксіома С II).

Найпростіші наслідки з аксіом стереометрії

Безпосередньо з аксіом стереометрії випливає чимало властивостей взаємного розміщення точок, прямих і площин. Розглянемо деякі з них.

Пряма а  належить  площині α (або лежить у площині α), якщо всі її точки належать даній прямій.

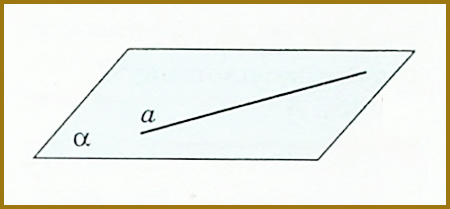
Розглянемо наступний малюнок:

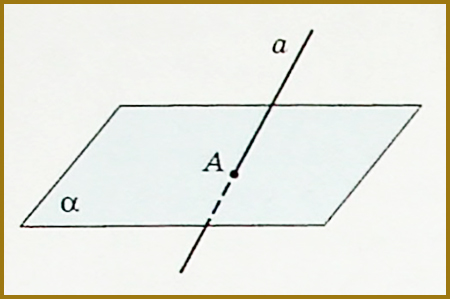
З аксіоми С II випливає, що пряма, яка не належить площині, має з цією площиною не більше від однієї спільної точки. 

Пряма перетинає площину, якщо пряма і площина мають єдину спільну точку.

Додаткова інформація до аксіоми проведення площини (аксіома С IV)

Поряд із формулюванням “три точки належать одній площині” в стереометрії часто кажуть і про чотири точки (декілька точок, прямі, фігури тощо), що не лежать в одній площині. Таке формулювання означає, що неможливо провести площину, яка містила б усі дані точки (прямі, фігури). Доведемо це.

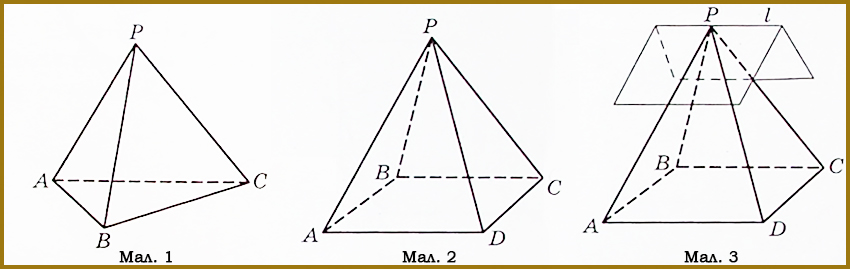
Наприклад, вершини Р, А, В і С тетраедра РАВС не лежать в одній площині (мал. 1), хоча будь-які три з них належать одній площині.

Звернемось тепер до розгляду взаємного розміщення двох площин. Для цього розглянемо чотирикутну піраміду PABCD, основа якої – прямокутник ABCD (мал. 2), і спробуємо визначити, скільки спільних точок мають площини PAD і PBC. На перший погляд відповідь очевидна: одну – точку Р. Але така відповідь є невірною.

Аби переконатися в цьому, прикладемо зігнутий аркуш паперу до піраміди так, щоб одна його частина лежала на грані PAD, а інша — на грані РВС (мал. 3). При такому моделюванні стає зрозумілим, що всі точки прямої і перегину аркуша (у тому числі, й точка Р) є спільними точками площин PAD і РВС.

Використана література:

1. Роганін О. М. Математика: Посібник для школярів та абітурієнтів. – Х. : Гімназія, 2010. – 471 с. : іл.
2. Математика. Довідник + тести. Повний повторювальний курс, підготовка до зовнішнього незалежного оцінювання та державної підсумкової атестації/ Олександр Істер. – Кам’янець-Подільський: ФОП Сисин О. В., 2021. – 540 с.
3. Математика 10-11: Підруч. для шк., ліцеїв та гімназій гуманіт. профілю/ М. І. Бурда, Ю. І. Мальваний, О. С. Дубинчук. – К. : Освіта, 2006. – 287 с.
4. Геометрія: (проф. рівень) : підруч. для 10-го кл. закл. заг. серед. освіти / О. С. Істер, О. В. Єргіна. – Київ : Генеза, 2018. – 368 с. : іл.