Ірраціональні рівняння. Методи розв’язування

Сьогодні ми розглянемо ірраціональні рівняння та методи їх розв’язування.

Рівняння називають ірраціональним, якщо воно містить змінну під знаком кореня.

Піднесення обох частин рівняння до одного степеня

При піднесенні обох частин рівняння до непарного степеня одержуємо рівняння, рівносильне заданому (на його ОДЗ).

При піднесенні ж обох частин рівняння до парного степеня отримуємо рівняння-наслідки, де можуть з’явитися сторонні корені, які відсіюються перевіркою.

\[ Рівняння\ {\sqrt[n]{х}, \ n \in \ N , \ n\geq 2} \]

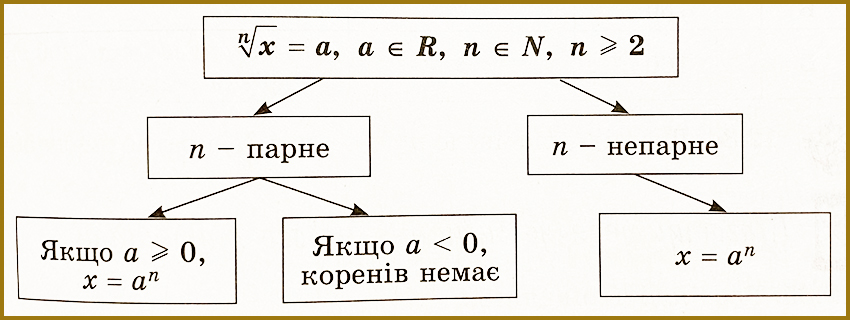
Якщо а ≥ 0, то таке рівняння має розв’язки. Якщо а < 0, то рівняння коренів не має.

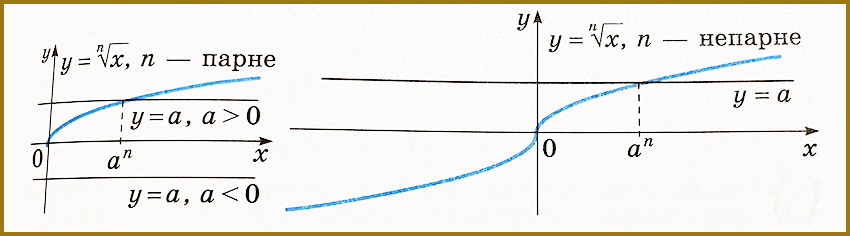
Якщо n – непарне, то для будь-якого значення а рівняння має тільки один корінь.

Приклади розв’язання

1)

\[ \sqrt{х}=-2 \]

Рівняння коренів не має.

2)

\[ \sqrt[4]{х}=-1 \]

Рівняння коренів не має.

3)

\[ \sqrt[5]{х}=-1 \]

\[ ({\sqrt[5]{х}})^5=({-1})^5 \]

\[ х=-1 \]

4)

\[ \sqrt[7]{х}=-2 \]

\[ ({\sqrt[7]{х}})^7=({-2})^7 \]

\[ х=-128 \]

5)

\[ \sqrt{х}=5 \]

\[ ({\sqrt{х}})^2=5^2 \]

\[ х=25 \]

6)

\[ \sqrt[3]{х}=1 \]

\[ ({\sqrt[3]{х}})^3=1^3 \]

\[ х=1 \]

7)

\[ \sqrt[3]{х}=2 \]

\[ ({\sqrt[3]{х}})^3=2^3 \]

\[ х=8 \]

8)

\[ \sqrt[4]{х}=2 \]

\[ ({\sqrt[4]{х}})^4=2^4 \]

\[ х=16 \]

9)

\[ \sqrt[6]{х}=0 \]

\[ ({\sqrt[6]{х}})^6=0^6 \]

\[ х=0 \]

Отже, коли ми розв’язуємо ірраціональні рівняння, то звертаємо увагу на те, що парний показник кореня не може бути з від’ємною відповіддю.

Розглянемо наступні, дещо складніші ірраціональні рівняння.

\[ Рівняння \ вигляду\ \sqrt[n]{f(х)}=g(х), \ n \in \ N , \ n\geq 2 \]

Загальним методом розв’язування таких ірраціональних рівнянь є піднесення їх лівої і правої частин до степеня n.

У випадку непарного n рівняння

\[ \sqrt[n]{f(х)}=g(х) \]

буде рівносильне рівнянню

\[ f(х)=g^n(х), \ де \ g^n(х)=(g(х))^n. \]

Якщо ж n – непарне число, то ліва частина рівняння

\[ \sqrt[n]{f(х)}=g(х) \]

є невід’ємною, тому невід’ємною має бути і права його частина. Отже, для рівносильних перетворень рівняння умова g(х)≥0 є обов’язковою. Після піднесення обох частин рівняння до степеня n, отримаємо 

\[ f(х)=g^n(х),\ де \ g^n(х)\geq 0 \]

(оскільки  n – парне), тому f(х)≥0. Отже у випадку парного n рівняння рівносильне системі

\[ \begin{cases} {f(х)={g^n(х),}} \\ {g(х)\geq{0}.} \end{cases} \]

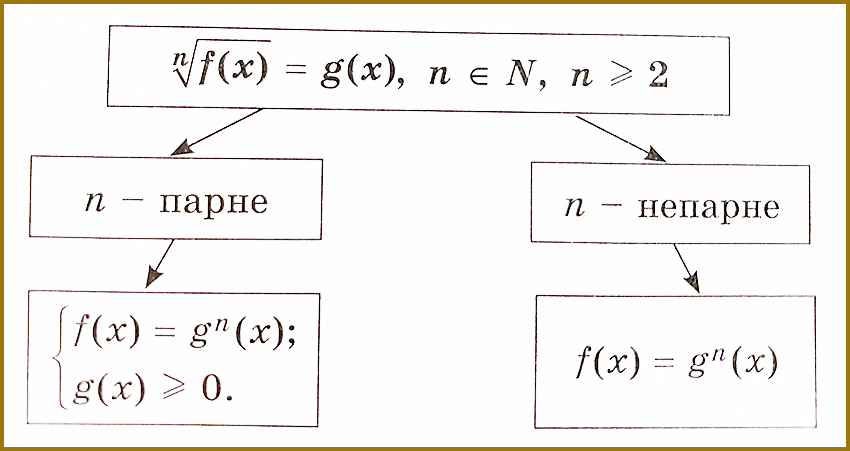
Пригадуємо, що з цієї рівності, де n – парне число автоматично випливає, що f(х)≥0.

Приклади розв’язання

1)

\[ \sqrt[4]{х+1}=1 \]

\[ ({\sqrt[4]{х+1}})^4=1^4 \]

\[ х+1=1 \]

\[ х=1-1 \]

\[ х=0 \]

Перевірка: 0+1=1

2)

\[ \sqrt[4]{х+2}=1 \]

\[ ({\sqrt[4]{х+2}})^4=1^4 \]

\[ х+2=1 \]

\[ Х=1-2 \]

\[ Х=-1 \]

Перевірка: -1+2=1.

3)

\[ \sqrt{х-7}=2 \]

\[ ({\sqrt{х-7}})^2=2^2 \]

\[ х-7=4 \]

\[ х=4+7 \]

\[ х=11 \]

Перевірка: 11-7=4.

4)

\[ \sqrt[8]{2х-4}=2 \]

\[ ({\sqrt[8]{2х-4}})^8=2^8 \]

\[ 2х-4=256 \]

\[ 2х=256+4 \]

\[ 2х=260 \]

\[ х={\frac{260}{2}} \]

\[ х=130 \]

\[ Перевірка: \sqrt[8]{2\times 130-4}=2 \]

\[ 2=2 \]

5)

\[ \sqrt[6]{х+3}=-1 \]

Рівняння коренів не має.

6)

\[ \sqrt[5]{х^2-1}=-1 \]

\[ ({\sqrt[5]{х^2-1}})^5=({-1})^5 \]

\[ х^2 -1=-1 \]

\[ х^2 =-1+1 \]

\[ х^2 =0 \]

\[ х=0 \]

\[ Перевірка: ({\sqrt[5]{0^2-1}})^5=-1 \]

\[ \sqrt[5]{-1}=-1 \]

\[ -1=-1 \]

7)

\[ \sqrt[4]{х^2-9}=0 \]

\[ х^2-9=0 \]

Ми отримали неповне квадратне рівняння.

\[ х^2 =9 \]

\[ х_{1}=\sqrt{9}=3 \]

\[ х_{2}=-\sqrt{9}=-3 \]

\[ Перевірка: \sqrt[4]{3^2-9}=\sqrt[4]{9-9}=\sqrt[4]{0}=0 \]

\[ \sqrt[4]{({-3})^2-9}=\sqrt[4]{9-9}=\sqrt[4]{0}=0 \]

\[ Відповідь: х_{1}=3, х_{2}=-3. \]

8)

\[ \sqrt[7]{х^2 -3}=1 \]

\[ ({\sqrt[7]{х^2-3}})^7=1^7 \]

\[ х^2-3=1 \]

\[ х^2=1+3 \]

\[ х^2=4 \]

\[ х_{1}=\sqrt{4}=2 \]

\[ х_{2}=-\sqrt{4}=-2 \]

\[ Перевірка: 2^2-3=1\\ 4-3=1 \]

\[ 1=1 \]

\[ ({-2})^2-3=1 \\ 4-3=1 \]

\[ 1=1 \]

\[ Відповідь: х_{1}=2, х_{2}=-2. \]

9)

\[ \sqrt{х^2 +8х}=3 \\ (\sqrt{х^2 +8х})^2=3 ^2 \]

\[ х^2+8х=9 \]

\[ х^2+8х-9=0 \]

Виходить повне квадратне рівняння, де а=1, в=8, с=-9. Пригадуємо теорему Вієта:

\[ \begin{cases} {х_{1}}+{х_{2}={-\frac{в}{а}={-\frac{8}{1}=-8}}} \\ {х_{1}}\times{х_{2}={\frac{с}{а}={-\frac{9}{1}=-9}}} \end{cases} \]

Тепер нам потрібно знайти такі два числа, які при множенні дадуть -9 і при додаванні дадуть -8.

Яка пара чисел при множенні дасть -9?

\[ {1\times({-9})}=-9 \]

Тепер визначимо, яка пара чисел дасть у сумі -8?

\[ -9+1=-8 \]

Отже, коренями рівняння є

\[ х_{1}=-9 \]

\[ х_{2}=1 \]

Тепер перевіримо, чи ці значення задовольняють початкове рівняння.

\[ {\sqrt{({-9})^2+8\times({-9})}}=\sqrt{81-72}=\sqrt{9}=3 \]

3=3, тож це підходить.

\[ {\sqrt{(1)^2+8\times1}}=\sqrt{1+8}=\sqrt{9}=3 \]

Це також підходить.

Відповідь:

Розв’язками цього рівняння є:  х=-9, х=1.

10)

\[ \sqrt[3]{х^2+4}=0 \]

\[ ({\sqrt[3]{х^2+4}})^3=0^3 \]

\[ х^2+4=0 \]

\[ х^2=-4 \]

Рівняння розв’язку не має.

11)

\[ \sqrt{х^2 -3х}=2 \]

\[ ({\sqrt{х^2-3х}})^2=2^2 \]

\[ х^2-3х=4 \]

\[ х^2-3х-4=0 \]

а=1, в=-3, с=-4

\[ \begin{cases} {х_{1}}+{х_{2}={-\frac{в}{а}={-\frac{-3}{1}=3}}} \\ {х_{1}}\times{х_{2}={\frac{с}{а}={\frac{-4}{1}=-4}}} \end{cases} \]

Знаходимо корені рівняння.

Потрібно знайти два числа, які у сумі дадуть 3, а у добутку дадуть -4.

4+(-1)=3

Поміркуємо, для того щоб отримати від’ємне число у добутку, одне з чих чисел має бути додатним, а інше від’ємним. Бо якщо взяти обидва числа додатними (наприклад, 4 і 1) або обидва від’ємні (наприклад, -4 і -1), то добуток не буде дорівнювати -4. Отже, тільки пара 4 і -1 дасть нам правильний добуток.

\[ 4\times(-1)=-4 \]

Таким чином, коренями рівняння є: х=4, х=-1.

Робимо перевірку:

\[ {\sqrt{4^2-3\times4}}=\sqrt{16-12}=\sqrt{4}=2 \]

Це підходить.

\[ {\sqrt{({-1})^2-3\times({-1})}}=\sqrt{1+3}=\sqrt{4}=2 \]

Це теж підходить.

Відповідь: розв’язки рівняння х=4 і х=-1.

12)

\[ \sqrt{-х^2 -6х+8}-х=6 \\ \sqrt{-х^2 -6х+8}=6+х \\ Знаходимо\ ОДЗ: \ 6+х\geq 0 \\Тоді,\ х\geq-6 \\ -х^2 -6х+8=(6+х)^2 \\ -х^2 -6х+8=36+12х+х^2 \\ -х^2 -6х+8-36-12х-х^2=0 \\ -2х^2-18х-28=0 \quad{\mid} :(-2) \\ х^2 +9х+14=0 \\ а=1; \ в=9; \ с=14 \\ \begin{cases} {х_{1}}+{х_{2}={-\frac{в}{а}={-\frac{9}{1}=-9}}} \\ {х_{1}}\times{х_{2}={\frac{с}{а}={\frac{14}{1}=14}}} \end{cases} \]

\[ -7\times(-2)=14 \\ -7+(-2)=-9 \\ {х_{1}}=-7 \quad {х_{2}}=-2 \]

Відповідь: х=-2.

13)

\[ \sqrt{-х^2 -8х+9}-х=5 \\ \sqrt{-х^2 -8х+9}=5+х \\Знаходимо\ ОДЗ: \ 5+х\geq 0 \\Тоді,\ х\geq-5 \\ -х^2 -8х+9=(5+х)^2 \\ -х^2 -8х+9=25+10х+х^2 \\ -2х^2-18х-16=0 \quad{\mid}:(-2) \\ х^2+9х+8=0 \\ -8+(-1)=-9 \\ -8\times(-1)=8\\ {х_{1}}=-8 \quad {х_{2}}=-1 \]

Відповідь: х=-1.

\[ Більш \ складні \ рівняння \ вигляду \ \sqrt[n]{f(х)}=g(х) \]

Розв’яжіть рівняння

14)

\[ х+4=\sqrt{4-6х-2^2} \]

\[ (х+4)^2=({\sqrt{4-6х-х^2}})^2 \]

\[ (х+4)^2={{4-6х-х^2}} \]

\[ \begin{cases} {х+4\geq{0}} & \quad\text{ ОДЗ} \\х\geq-4 \end{cases} \]

\[ Використовуємо\ формулу: (а+в)^2=а^2+2ав+в^2 \]

\[ х^2+8х+16=4-6х-х^2 \]

\[ х^2+8х+16-4+6х+х^2=0 \]

\[ 2х^2+14х+12=0 {\quad\text{ 1:2}} \\х^2+7х+6=0 \]

Далі можна скористатися формулою Вієта, де а=1, в=7, с=6

\[ \begin{cases} {х_{1}}+{х_{2}={-\frac{в}{а}={-\frac{7}{1}=-7}}} \\ {х_{1}}\times{х_{2}={\frac{с}{а}={\frac{6}{1}=6}}} \end{cases} \]

Знаходимо корені рівняння. Це будуть числа -6 і -1, щоб задовільнити умови

\[ -1\times (-6)=6 \\-1+(-6)=-7 \]

Отже розв’язком даного рівняння є:

\[ х_{1}=-6\\ х_{2}=-1 \]

Можна при розв’язуванні данного ірраціонального рівняння піти й іншим шляхом, тоді

\[ х^2+7х+6=0 \\х^2+х+6х+6=0 \\х(х+1)+6(х+1)=0 \\(х+1)\times(х+6)=0 \\х+1=0 {\quad\text{ х+6=0}} \\х=-1 {\quad\text{ х= -6}} \]

Як бачимо, корені рівняння зійшлися з нашим минулим рішенням. Тож, вибирайте найзручніший для себе хід розв’язку.

Тепер згадаймо ОДЗ данного рівняння, де відповідь повинна бути більшою ніж -4, або дорівнювати цьому числу. Отже, нам підійде лише -1.

Відповідь: розв’язком рівняння є х=-1.

15)

\[ \sqrt{3-х}=х-1 \\ х-1\geq 0\impliesх\geq 1 \quad\text{ ОДЗ} \\ (\sqrt{3-х})^2=(х-1)^2 \\ 3-х=х^2-2х+1 \\ 3-х-х^2+2х-1=0 \\ -х^2+х+2=0 \]

Змінюємо знаки на протилежні:

\[ х^2-х-2=0 \\ а=1; \ в=-1; \ с=-2 \\ \begin{cases} {х_{1}}+{х_{2}={-\frac{в}{а}={-\frac{-1}{1}=1}}} \\ {х_{1}}\times{х_{2}={\frac{с}{а}={\frac{-2}{1}=-2}}} \end{cases} \\ 2\times(-1)=-2 \\ 2+(-1)=1 \]

\[ Перевірка: \sqrt{3-2}=2-1 \\ \sqrt{1}=1 \\ 1=1 \]

Тому, х=2 є коренем рівняння.

Можна з отриманого вище квадратного рівняння знайти корені іншим шляхом. Роздивимось докладніше:

\[ х^2-х-2=0 \]

\[ Де \ -х \ запишемо \ як \ х-2х. Тоді, \\ х^2+х-2х-2=0 \\ х(х+1)-2х-2=0 \\ х(х+1)-2(х+1)=0 \\ (х+1)(х-2)=0 \\ х+1=0 \quad{х-2=0} \\ х=-1 \quad{х=2} \]

Відповідь: х=2, тому що задовольняє ОДЗ і розв’язок рівняння.

16)

\[ \sqrt{3+х}=х+1 \\ х+1\geq 0\impliesх\geq -1 \quad\text{ ОДЗ} \\ (\sqrt{3+х})^2=(х+1)^2 \\ (а+в)^2=а^2+2ав+в^2 \\ 3+х=х^2+2+1 \\ 3+х-х^2-2х-1=0 \\ -х^2-х+2=0 \]

Змінюємо знаки:

\[ х^2+х-2=0 \\ а=1; \ в=1; \ с=-2 \\ \begin{cases} {х_{1}}+{х_{2}={-\frac{в}{а}={-\frac{1}{1}=-1}}} \\ {х_{1}}\times{х_{2}={\frac{с}{а}={\frac{-2}{1}=-2}}} \end{cases} \\ -2+1=-1 \\ -2\times1=-2 \]

Або знаходимо корені рівняння таким шляхом:

\[ х^2+2х-х-2=0 \\ х(х+2)-х-2=0 \\ х(х+2)-(х+2)=0 \\ х(х+2)\times(х-1)=0 \\ х+2=0 \quad{ х-1=0 } \\ х=-2 \quad{ х=1 } \]

Перевірка: 

\[ \sqrt{3+1}=1+1 \\2=2 \]

Відповідь: х=1.

\[ Рівняння \ вигляду \sqrt[n]{f(х)}=\sqrt[n]{g(х)}, \ n \in \ N , \ n\geq 2 \]

Звідси випливає, що f(х)=g(х). У випадку непарного n функції f(х) і g(х) можуть набувати будь-яких значень.

Якщо ж n парне, то областю допустимих значень рівняння є такі значення  х, для  яких одночасно справджуються умови  f(х)≥0 і g(х)≥0. Тому у випадку парного n рівняння

\[ \sqrt[n]{f(х)}=\sqrt[n]{g(х)} \]

буде рівносильне одній з систем

\[ \begin{cases} {f(х)={g(х),}} \\ {f(х)\geq{0}} \quad\text{ або} \end{cases} \]

\[ \begin{cases} {f(х)={g(х),}} \\ {g(х)\geq{0.}} \end{cases} \]

Записуючи систему для розв’язання рівняння

\[ \sqrt[n]{f(х)}=\sqrt[n]{g(х),} \]

яку саме з двох нерівностей f(х)≥0 або g(х)≥0 вибирати залежить від того, яку з них буде легше розв’язати.

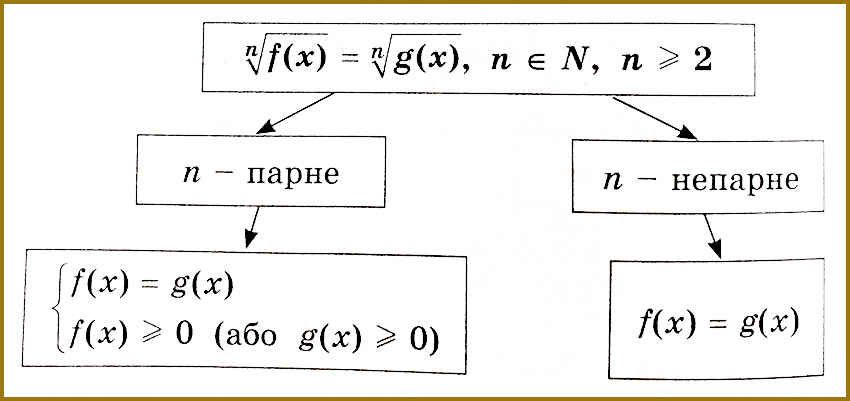
Розв’язати ірраціональне рівняння

1)

\[ \sqrt[5]{3х-2}=\sqrt[5]{2х+11} \\ (\sqrt[5]{3х-2})^5=(\sqrt[5]{2х+11})^5 \\ 3х-2=2х+11 \\ 3х-2-2х-11=0 \\ х-13=0 \\ х=13 \]

2)

\[ \sqrt[4]{х^2+2х}=\sqrt[4]{3х+2} \]

Рівняння рівносильне системі:

\[ \begin{cases} {х^2+2х={3х+2,}} \\ {3х+2\geq{0;}} \end{cases} \]

\[ Тобто \begin{cases} {х^2-х-2=0} \\ {х\geq{-\frac{2}{3};}} \end{cases} \]

звідки маємо х=2, тому що

\[ х^2-х-2=0 \\ а=1; \ в=-1; \ с=-2 \]

\[ \begin{cases} {х_{1}}+{х_{2}={-\frac{в}{а}={-\frac{-1}{1}=1}}} \\ {х_{1}}\times{х_{2}={\frac{с}{а}={\frac{-2}{1}=-2}}} \end{cases} \\ 2\times(-1)=-2 \\ 2+(-1)=1 \\ х_{1}=2,\ х_{2}=-1 \\ Відповідь: \ х=2. \]

Розв’язування ірраціональних рівнянь, що містять кілька квадратних коренів

\[ \sqrt{f(х)}\pm\sqrt{g(х)}=а \]

Де а – деяке число.

\[ \sqrt{f(х)}\pm\sqrt{g(х)}=\sqrt{t(х)} \]

 та їм подібні ірраціональні рівняння доцільно починати зі знаходження ОДЗ рівняння, а опісля скористатися одним із нижченаведених способів розв’язування.

Приклади розв’язання 

1)

\[ \sqrt{х+3}+\sqrt{х+8}=5 \]

\[ \begin{cases} {х+3\geq{0}} \\ {х+8\geq{0}} & \quad\text{ ОДЗ. } \end{cases} \\Тобто, х\geq{3}. \]

Оскільки права частина останнього рівняння може бути як додатною, так і від’ємною, то таке перетворення не є рівносильним, тому отриманий корінь слід перевірити.

\[ ({\sqrt{х+3}})^2=(5-{\sqrt{х+8}})^2 \]

Застосуємо формулу:

\[ (а-в)^2=а^2-2ав+в^2 \]

\[ х+3=5^2-2\times 5\sqrt{х+8}+(\sqrt{х+8})^2 \\ х+3=25-10\sqrt{х+8}+х+8 \\ 3-25+10\sqrt{х+8}-8=0 \\ -30+10\sqrt{х+8}=0 \ \quad\text{ :10} \\ -3+\sqrt{х+8}=0 \\ \sqrt{х+8}=3 \\({\sqrt{х+8}})^2=3^2 \\ х+8=9 \\ х=9-8 \\ х=1 \]

Перевірка:

\[ \sqrt{1+3}+\sqrt{1+8}=2+3=5 \]

Відповідь: 1.

2)

\[ \sqrt{2х+3}+\sqrt{3х+2}=\sqrt{2х+5}+\sqrt{3х} \]

Знайдемо ОДЗ рівняння:

\[ \begin{cases} {2х+3\geq{0}} \\ {3х+2\geq{0}} \implies\\ {2х+5\geq{0}}\\ {3х\geq{0}} \end{cases} \]

\[ \begin{cases} {2х\geq{-3}} \\ {3х\geq{-2}} \implies\\ {2х\geq{-5}}\\ {3х\geq{0}} \end{cases} \]

\[ \begin{cases} {х\geq-\frac{3}{2}} \\ {х\geq-\frac{2}{3}} \\ {х\geq-\frac{5}{2}} \\ {х\geq{0}} \end{cases} \\Тобто, х\geq{0}. \]

\[ (\sqrt{2х+3}+\sqrt{3х+2})^2=(\sqrt{2х+5}+\sqrt{3х})^2 \\ (а+в)^2=а^2+2ав+в^2 \\ 2х+3+2\times\sqrt{{(2х+3)}\times{(3х+2)}}+3х+2=2х+5+2\times\sqrt{{(2х+5)}\times{(3х)}}+3х \\ 2\times\sqrt{{(2х+3)}\times{(3х+2)}}=2\times\sqrt{{(2х+5)}\times{(3х)}} \quad\text{:2} \\ (\sqrt{{(2х+3)}\times{(3х+2)}})^2=(\sqrt{{(2х+5)}\times{(3х)}})^2 \\ (2х+3)\times(3х+2)=(2х+5)\times(3х)\\ 6х^2+4х+9х+6=6х^2+15х \\ 13х+6=15х \\ 13х-15х=-6 \\ -2х=-6 \\ 2х=6 \\ х=\frac{6}{2} \\ х=3 \]

3)

\[ \sqrt{5х +5}+\sqrt{2х +1}=\sqrt{3х +4} \]

Знайдемо ОДЗ рівняння, розв’язавши систему нерівностей:

\[ \begin{cases} {5х+5\geq{0}} \\ {2х+1\geq{0}}\implies \\ {3х+4\geq{0}} \end{cases} \]

\[ \begin{cases} {5х\geq{-5}} \\ {2х\geq{-1}}\implies \\ {3х\geq{-4}} \end{cases} \]

\[ \begin{cases} {х\geq-\frac{5}{5}} \\ {х\geq-\frac{1}{2}} \\ {х\geq-\frac{4}{3}} \end{cases} \\Тобто, х\geq{-0,5}. \]

Обидві частині рівняння є невід’ємними. Аби не робити громіздких обчислень при піднесенні їх до квадрата, можна зробити наступне:

\[ \sqrt{5х+5}=\sqrt{3х+4}-\sqrt{2х+1} \]

Таке рівняння рівносильне системі:

\[ \begin{cases} {\sqrt{(5х+5)^2}=(\sqrt{(3х+4)}-\sqrt{(2х+1)}})^2, \\ \sqrt{3х+4}- \sqrt{2х+1}\geq 0 \end{cases} \]

\[ \begin{cases} {5х+5=3х+4-2\sqrt{3х+4}\times\sqrt{2х+1}+2х+1}, \\ \sqrt{3х+4}\geq \sqrt{2х+1}; \end{cases} \]

\[ \begin{cases} {2\sqrt{3х+4}\times \sqrt{2х+1}=0}, \\ \sqrt{3х+4}\geq \sqrt{2х+1}; \end{cases} \]

\[ \begin{cases} {\sqrt{3х+4}\times \sqrt{2х+1}=0}, \\ \ х \geq -3. \end{cases} \]

Перше рівняння має корені

\[ х_{1}=-\frac{4}{3}, \ х_{1}=-0,5. \]

Але лише другий задовольняє як умову

\[ х\geq-3, \]

так і ОДЗ рівняння. Оскільки всі перетворення були рівносильними, то перевірка не є обов’язковою.

Відповідь: -0,5.

Метод заміни змінної в ірраціональному рівнянні

Якщо до рівняння змінна входить в одному й тому самому вигляді, то буде зручно відповідний вираз із змінною позначити однією буквою (новою змінною).

\[ \sqrt[n]{f(х)}=t \]

Приклади розв’язання

1) Розв’яжіть ірраціональне рівняння

\[ \sqrt[3]{х-2}-5\sqrt[6]{х-2}+6=0 \\ Нехай\ \sqrt[6]{х-2}=t, тоді \\ \sqrt[3]{х-2}=\sqrt[6]{(х-2)^2}=(\sqrt[6]{х-2})^2=t^2. \]

Отже, маємо рівняння:

\[ t^2-5t+6=0 \\ t=\frac{-в \pm\sqrt{в^2-4ас} }{2а},\ де \\ а=1; \ в=-5; \ с=6. \]

Знайдемо дискримінант:

\[ D=в^2-4ас= (-5)^2-4\times1\times 6=25-24=1 \\ t=\frac{-(-5)\pm\sqrt{1}}{2\times1}=\frac{5\pm 1}{2} \\ {t_{1}}=\frac{5+1}{2}=\frac{6}{2}=3 \\ {t_{2}}=\frac{5-1}{2}=\frac{4}{2}=2 \]

\[ Корені\ рівняння:\ {t_{1}}=3, \ {t_{2}}=2. \]

Обидва корені задовольняють умову t≥0. Повертаємося до заміни:

\[ 1) \ якщо \ t=2, то \ \sqrt[6]{х-2}=2, \ тоді \ х=66.\\ \sqrt[6]{66-2}=2 \\ \sqrt[6]{64}=2 \\ 2=2 \\ 2) \ якщо \ t=3, то \ \sqrt[6]{х-2}=3, \ тоді \ х=731.\\ \sqrt[6]{731-2}=3 \\ \sqrt[6]{729}=3 \\ 3=3 \]

Відповідь: 66; 731.

2) Розв’яжіть ірраціональне рівняння

\[ \sqrt[3]{х^2}+\sqrt[3]{х}=2 \\ Позначимо \ \sqrt[3]{х}=t, \ тоді \\ \sqrt[3]{х^2}=(\sqrt[3]{х})^2=t^2. \]

\[ Одержуємо \ рівняння \ t^2+t=2 \\ t^2+t-2=0 \\ а=1; \ в=1; \ с=-2 \\ \begin{cases} {х_{1}}+{х_{2}={-\frac{в}{а}={-\frac{1}{1}=-1}}} \\ {х_{1}}\times{х_{2}={\frac{с}{а}={\frac{-2}{1}=-2}}} \end{cases} \\ -2+1=-1\quad {-2\times1=-2} \\ {t_{1}}=1, \ {t_{2}}=-2. \]

Виконуємо обернену заміну: 

\[ \sqrt[3]{х}=1, тоді \ х=1 \ або \ \sqrt[3]{х}=-2, \ звідси \ х=-8. \]

Відповідь: 1; -8.

Використання теореми про рівносильність

Якщо обидві частини рівняння невід’ємні, то при піднесенні обох частин рівняння до парного степеня одержуємо рівняння, рівносильне заданому, за умови урахування його ОДЗ.

\[ \sqrt[2n]{f(х)}=g(х)\Leftrightarrow\begin{cases} {g(х)\geq}0, \\ {f(х)\geq{g^{2n}(х)}} \end{cases} \]

Приклади розв’язання

\[ \sqrt[3]{х-2}+\sqrt{х+1}=3 \\ Нехай \ \begin{cases} {\sqrt[3]{х-2}={u}} \\ {\sqrt{х+1}={v}}. \end{cases} \]

\[ Тоді \ \begin{cases} {х-2=u^3} \\ {х+1=v^2}. \end{cases} \]

Адже після заміни

\[ \sqrt[3]{х-2}=u \ та \ \sqrt{х+1}=v \]

із заданого рівняння ми отримали одне рівняння u+v=3. ТО для того аби одержати друге рівняння, ми записали за означенням кореня n-го степеня. Таким чином одержуючи систему рівнянь

\[ \begin{cases} {u+v=3} \\ {u^3-v^2=-3}. \end{cases} \]

Із першого рівняння знаходимо v=3-u і підставляємо в друге рівняння:

\[ u^3-(3-u)^2=-3 \\ (а-в)^2=а^2-2ав+в^2 \\ u^3-(9-6u+u^2)=-3 \\ u^3-u^2+6u-6=0 \\ u^2(u-1)+6(u-1)=0 \\ (u-1)(u^2+6)=0 \]

\[ Ураховуючи, \ що \ u^2=6\neq 0, \]

одержуємо u=1. Тоді v=2, оскільки

\[ х-2=1^3 \\ х=1^3+2 \\ х=1+2=3. \\ Звідси \ отримуємо \ 3+1=2^2 \]

Маємо систему рівнянь

\[ \begin{cases} {\sqrt[3]{х-2}=1} \\ {\sqrt{х+1}=2} \end{cases} \]

Із першого рівняння отримуємо х=3, тому що

\[ \sqrt[3]{х-2}=1 \\ (\sqrt[3]{х-2})^3=1^3 \\ х-2=1 \\ х=1+2 \\ х=3. \]

Це задовольняє і друге рівняння: 

\[ \sqrt{3+1}=2 \\ \sqrt{4}=2 \\ 2=2 \]

Відповідь: 3.

 Розв’язування ірраціональних рівнянь з параметрами

1)

\[ (а^2-1)\sqrt[6]{х}=а-1 \]

Розглянемо два випадки:

\[ а^2-1=0 \ і \ а^2-1\neq 0. \]

1. \[ Нехай \ а^2-1=0, \]

   тоді а=1 або а=-1. Якщо а=1, маємо рівняння:

\[ 0\times\sqrt[6]{х}=0, \]

тоді коренем буде будь-яке число з ОДЗ рівняння. Отже, х≥0. Якщо а=-1, маємо рівняння:

\[ 0\times\sqrt[6]{х}=-2, \]

яке не має коренів.

2.

\[ Нехай \ а^2-1\neq 0, \ тобто \\ а\neq 1; \ а\neq -1. \ Тоді \ \sqrt[6]{х}=\frac{а-1}{а^2-1}; \\ тобто \ \sqrt[6]{х}=\frac{а-1}{а+1}. \]

Якщо а+1>0, тобто а>-1, то

\[ х=\frac{1}{(а+1)^6}. \]

Якщо а+1<0, тобто а<-1, то рівняння не має коренів.

Відповідь: якщо а≤-1, коренів не має; якщо а=1, то х≥0; якщо -1<а<1, то

\[ х=\frac{1}{(а+1)^6}. \]

2)

Скільки коренів залежно від значень параметра а має рівняння

\[ (х+а)\sqrt{х^2-3х+2}=0 \ ? \]

ОДЗ рівняння знайдемо з умови

\[ х^2-3х+2\geq 0, \\ тобто \ (х-1)(х-2)\geq 0. \\ Отже \ х \in \ (-\infty;1] \ \cup \ [2;+\infty). \]

Розв’язуючи рівняння, отримаємо корені 

\[ х_{1}=1 \ і \ х_{2}=2 \]

для будь-якого значення параметра а та корінь х=-а. Останній корінь має задовольнити ОДЗ, тобто -а≤1 або -а≥2, що справджується за умови: а≥-1 або а≤-2.

Якщо а=-1 або а=-2, то отримаємо корінь, що збігатиметься з раніше знайденим (х=1 та х=2).

Якщо ж а<-2 або а>-1, то

\[ х_{3}=-а \ – третій \ корінь \ рівняння. \]

Відповідь: якщо а<-2 або а>-1, то рівняння має три корені, а якщо -2≤а≤-1, то рівняння має два корені.

3)  Для всіх значень параметра а розв’яжіть рівняння

\[ \sqrt{х^2-6х+5}+\sqrt{х^2-7х+10}=а\sqrt{х-5} \\ \sqrt{(х-1)(х-5)} +\sqrt{(х-2)(х-5)}=а\sqrt{х-5} \]

ОДЗ рівняння: 

\[ х-5≥0 \\ х≥0, \]

для будь-якого значення а. Розглянемо х>5

\[ \sqrt{х-1}\times\sqrt{х-5}+\sqrt{х-2}\times\sqrt{х-5}=а\sqrt{х-5} \quad{\mid \ :\sqrt{х-5}} \\ \sqrt{х-1}+\sqrt{х-2}=а \\ Функція \ для \ у(х)= \sqrt{х-1}+\sqrt{х-2} \ для \ х\geq 5 \]

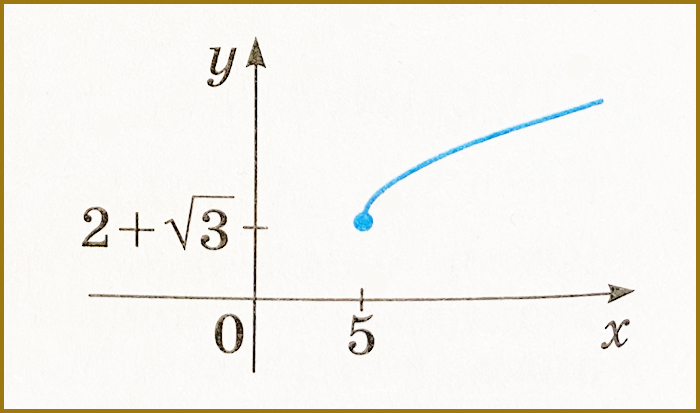
є зростаючою, як сума двох зростаючих функцій. Її найменше значення дорівнює у(5). Знайдемо це значення:

\[ у(5)=\sqrt{5-1}+\sqrt{5-2}=\sqrt{4}+\sqrt{3}=2+\sqrt{3}. \\ Рівняння \ а\geq 2+\sqrt{3} \ має \ один \ розв’язок \]

і не має розв’язків, якщо 

\[ а<2+\sqrt{3}. \]

Вернемось до рівняння: 

\[ \sqrt{х-1}+\sqrt{х-2}=а \\ \sqrt{х-2}=а-\sqrt{х-1} \\ (\sqrt{х-2})^2=(а-\sqrt{х-1})^2 \\ \begin{cases} {х-2=а^2-2а\sqrt{х-1}+х-1} \\ {а-\sqrt{х-1}\geq{0.}} \end{cases} \]

\[ Оскільки \ х-2=а^2-2а\sqrt{х-1}+х-1 \\ -2-а^2+2а\sqrt{х-1}+1=0 \\ -а^2+2а\sqrt{х-1}-1=0 \\ \sqrt{х-1}=\frac{1+а^2}{2а} \\ \begin{cases} {\sqrt{х-1}=\frac{1+а^2}{2а}} \\ {\sqrt{х-1}-а\leq{0},\ тоді} \end{cases} \]

\[ \frac{1+а^2}{2а}-а=\frac{1+а^2-2а^2}{2а}=\frac{1-а^2}{2а}\leq 0 \\ для \ а\geq 2+\sqrt{3}. \]

Отже, остаточно маємо:

\[ х-1=\bigg (\frac{1+а^2}{2а}\bigg)^2,\\ тоді \ х=1+\bigg (\frac{1+а^2}{2а}\bigg)^2. \]

Відповідь: 

\[ якщо \ а<2+\sqrt{3}, то \ х=5; \ якщо \ а\geq 2+\sqrt{3}, то \ х_{1}=5, \ х_{2}=\bigg(\frac{1+а^2}{2а}\bigg)^2. \]

4)

5)

Використані джерела: 

1) Алгебра і початки аналізу: (профіл. рівень) : підруч. для 10-го кл. закл. заг. серед. освіти / О. С. Істер, О. В. Єргіна. – Київ : Генеза, 2019. – 448 с. : іл.
2) Алгебра і початки аналізу: (профіл. рівень) : підруч. для 10-го кл. закл. заг. серед. освіти / Є. П. Нелін. – Харків : Вид-во “Ранок”, 2018. – 272 с.: іл.
3) naurok.com.ua

Щоб дізнаватися ще більше цікавого, підпишись на наші канали:

Не забудь підписатися на наші канали:

• Instagram 
• Facebook  
• Pinterest 
• YouTube